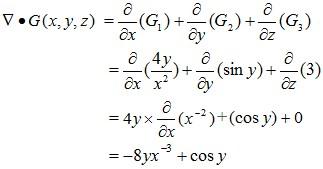Divergence of a Vector Field
A vector is a quantity that has a magnitude in a certain direction. Vectors are used to model forces, velocities, pressures, and many other physical phenomena. A vector field is a function that assigns a vector to every point in space. Vector fields are used to model force fields (gravity, electric and magnetic fields), fluid flow, etc.
The divergence of a vector field F = <P,Q,R> is defined as the partial derivative of P with respect to x plus the partial derivative of Q with respect to y plus the partial derivative of R with respect to z.
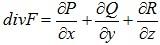
The divergence of a vector field is also given by:
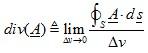
We define the divergence of a vector field at a point, as the net outward flux of per volume as the volume about the point tends to zero.
∇ ∙ A = divA
In Cartesian
∇ ∙ A ≡ ∂Ax/∂x + ∂Ay/∂y + ∂Az/∂z
In Cylindrical
∇ ∙ A ≡ ∂(r ∙ Ay)/(r ∙ ∂r) + ∂Aø/(r ∙ ∂ø) + ∂Az/∂z
In Spherical
∇ ∙ A ≡ ∂(R2 ∙ AR)/(R2∙∂R) + ∂(Aø ∙ sinθ)/(R ∙ sinθ ∙ ∂θ) + ∂Aø/(R ∙ sinθ ∙ ∂ø)
Example 1: Compute the divergence of F(x, y) = 3x2i + 2yj.
Solution: The divergence of F(x, y) is given by ∇•F(x, y) which is a dot product.
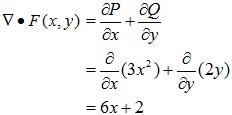
Example 2: Calculate the divergence of the vector field G(x,y,z) = exi + ln(xy)j + exyzk.
Solution: The divergence of G(x,y,z) is given by ∇• G(x,y,z) which is a dot product. Its components are given by:
G1 = ex
G2 = ln(xy)
G3 = exyz
and its divergence is:
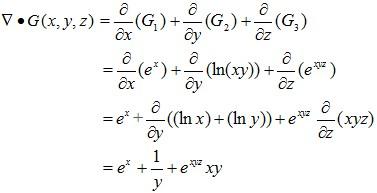
Example 3: Calculate the divergence of the vector field G(x, y, z) = 4y/x2 · i + (sin y)j + 3k
Solution: The divergence of G(x, y, z) is given by ∇• G(x,y,z) which is a dot product. Its components are given by:
G1 = 4y/x2
G2 = (sin y)
G3 = 3
and its divergence is