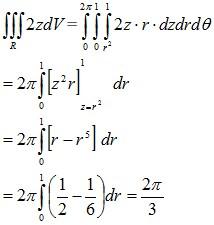Divergence Theorem/Gauss' Theorem
Let B be a solid region in R3 and let S be the surface of B, oriented with outwards pointing normal vector. Gauss Divergence theorem states that for a C1 vector field F, the following equation holds:
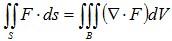
Note that for the theorem to hold, the orientation of the surface must be pointing outwards from the region B, otherwise we’ll get the minus sign in the above equation. Note that since S is the boundary of B, then it is always a closed surface ie: it has no boundary. In other words, the integral of a continuously differentiable vector field across a boundary (flux) is equal to the integral of the divergence of that vector field within the region enclosed by the boundary.
Applications of Gauss Theorem:
- The Aerodynamic Continuity Equation
- The surface integral of mass flux around a control volume without sources or sinks is equal to the rate of mass storage.
- If the flow at a particular point is incompressible, then the net velocity flux around the control volume must be zero.
- As net velocity flux at a point requires taking the limit of an integral, one instead merely calculates the divergence.
- If the divergence at that point is zero, then it is incompressible. If it is positive, the fluid is expanding, and vice versa.
- Gauss’s Theorem can be applied to any vector field which obeys an inverse-square law (except at the origin) such as gravity, electrostatic attraction, and even examples in quantum physics such as probability density.
Example 1: Use the divergence theorem to calculate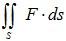 
, where S is the surface of the box B with vertices (±1, ±2, ±3) with outwards pointing normal vector and F(x, y, z) = (x2z3, 2xyz3, xz4).
Solution: Note that the surface integral will be difficult to compute, since there are six different components to parameterize (corresponding to the six sides of the box) and so one would have to compute six different integrals. Instead, using Gauss Theorem, it is easier to compute the integral (∇·F) of B.
First, we compute (∇·F) = 2xz3 + 2xz3 + 4xz3 = 8xz3. Now we integrate this function over the region B bounded by S:
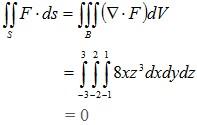
which is easy to verify.
Example 2: Evaluate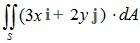 
, where S is the sphere given by x2 + y2 + z2 = 9.
Solution: We could parametrize the surface and evaluate the surface integral, but it is much faster to use the divergence theorem. Since
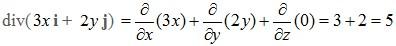
The divergence theorem gives:
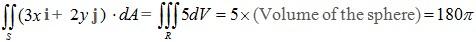
Example 3: Let R be the region in R3 by the paraboloid z = x2 + y2 and the plane z = 1and let S be the boundary of the region R. Evaluate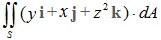 
Solution:
Since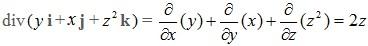 
The divergence theorem gives:
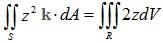
It is easiest to set up the triple integral in cylindrical coordinates:
