Definition of Identity Matrix
A square matrix in which all the main diagonal elements are 1’s and all the remaining elements are 0’s is called an Identity Matrix. Identity Matrix is also called Unit Matrix or Elementary Matrix. Identity Matrix is denoted with the letter “In×n”, where n×n represents the order of the matrix. One of the important properties of identity matrix is: A×In×n = A, where A is any square matrix of order n×n.
Examples of Identity Matrix
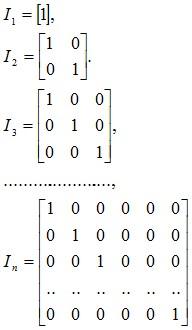
are identity matrices of order 1×1, 2×2, 3×3,………… n×n.
Example 1: Give an example of 4×4 order identity or unit matrix.
Solution:
We know that the identity matrix or unit matrix is the one with all ‘ones’ on the main diagonal and other entries as ‘zeros’. So the 4×4 order identity or unit matrix can be written as follows:

Example 2: Is the following matrix an Identity matrix?
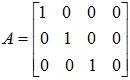
Solution:
No, the given matrix is not an identity matrix, because unit or identity matrix is a square matrix. In this case A is a matrix of order 3×4, which is not a square matrix.
Example 3: Is the following matrix a Unit matrix?
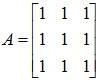
Solution:
No, the given matrix is not a unit matrix, since a unit matrix must only contain the value of 0 beside the diagonal values of 1.
Example 4: What is the multiplication of a matrix A by the identity matrix of order 5, given that A is a square matrix of order 5?
Solution:
We know that identity matrix is the one which satisfies A×In×n = A, where A is any square matrix of order n×n. Therefore the multiplication of a 5×5 matrix A by the identity matrix of order 5 is the same as A.