Current Location  >  Math Formulas > Geometry > Perimeter of a Polygon

Perimeter of a Polygon

Don't forget to try our free app - Agile Log , which helps you track your time spent on various projects and tasks, :)

Try It Now
Perimeter of a polygon:

A polygon is defined as a plane figure that is enclosed by closed path or a closed circle. Generally, perimeter is defined as path that surrounds an area. The perimeter of a polygon is the sum of the lengths of its sides.

Types of Polygons
·  Square
·  Rectangle
·  Parallelogram
·  Triangle
·  Rhombus
·  Trapezoid

List of polygon shapes

Shape

Description

 

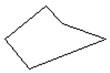
Polygon

A closed figure made of line segments each of which intersects with exactly two other line segments.

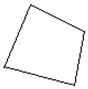
Quadrilateral

4-sided polygon

Square

A quadrilateral having all sides equal in length and forming right angles.

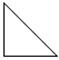
Triangle

A 3-sided polygon (sum of internal angles = 180°)

Rectangle

A 4-sided polygon with all right angles.

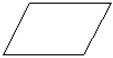
Parallelogram

4-sided polygon with two pairs of parallel sides.

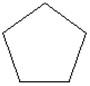
Pentagon

5-sided polygon (the graphic shows a regular hexagon with "regular" meaning each of the sides are equal in length)

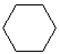
Hexagon

6-sided polygon

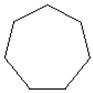
Heptagon

7-sided polygon

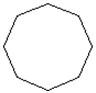
Octagon

8-sided polygon


Notes:
Perimeters of square and rhombus are equal
Perimeters of rectangle and parallelogram are equal
Perimeters of polygons with more than six sides can be found using the similar perimeter formula.
·  Heptagan (Polygon with seven sides) the perimeter is sum of the lengths of seven sides
·  Octagon (Polygon with eight sides) the perimeter is sum of the lengths of eight sides
·  Nenagon (Polygon with nine sides) the perimeter is sum of the lengths of nine sides
·  Decagon (Polygon with ten sides) the perimeter is sum of the lengths of ten sides

Shapes that are not considered as polygons:
The figure below is not a polygon, since it is not a closed figure:

The figure below is not a polygon, since it is not made of line segments:


The figure below is not a polygon, since its sides do not intersect in exactly two places each:


Regular Polygon:
A polygon that has all its sides equal with equal angles. The sum of the angles of a polygon with n sides, where n is 3 or more, is 180° × (n - 2) degrees.

Examples of regular polygons are: Equilateral triangle, Square and Rhombus

Perimeter of Regular Polygon is given by:
P = ns
Where n is the number of sides and s is the length of each side.

Irregular Polygon:
A polygon that has sides which are not equal and whose interior angles are different is called an irregular polygon.
Perimeter of an irregular polygon is determined by simply adding the length of each side together. The figures below show polygons that are not considered to be regular polygons:


Example 1: Find the perimeter of the following figure

Solution:
AB = FE + DC = 5 + 5 = 10 cm
BC = AF + ED = 4 + 4 = 8 cm

P = AB + BC + CD + DE + EF + FA
P = 10 + 8 + 5 + 4 + 5 + 4
P = 36 cm 


Example 2: Find the perimeter of regular decagon whose side is 5cm
Solution:
Number of sides in decagon (n) =10 and side s=5cm
Perimeter of decagon:
P = ns
P = 10 x 5
P = 50 cm


Example 3: Find the perimeter of dodecagon whose side is 7cm.
Solution:
Number of sides in dodecagon (n) =12 and side s=7cm
Perimeter of dodecagon:
P = ns
P = 12 x 7
P = 84 cm


Example 4: What is the perimeter of the figure below, if the area of the figure is 27 ft2?

Solution: The perimeter of the figure = AB + BD + DE + EA

·  The length of the side AB = 2 ft
·  The length of the side DE = 4 ft
·  The length of the side EA = 5 ft

The area of the trapezoid = ½ × height × (sum of the measures of the parallel sides)
Substituting the values we get:
Area = (12) × FC × (AE + BD)
Area = (12) × 3 × (5 + BD)


Since the area is given we now have:
27 ft2 = ½ × 3 × (5 + BD)

Multiply each side by 2
54 ft2 = 3 × (5 + BD)

Divide each side by 3
18 ft = 5 + BD

Subtracting 5 from both the sides
BD = 13 ft

And now we can determine the perimeter of the trapezoid:
The perimeter of the figure = 2 + 13 + 4 + 5 = 24 ft.

Example 5: Find the perimeter of the regular pentagon which is having the side length is 4 cm.
Solution:
We know that the perimeter of the regular polygon is given by: P = ns
Since pentagon has 5 sides, we have: n = 5
So the perimeter of the regular pentagon is 5 * 4 = 20 cm.


Example 6: What is the perimeter of a regular hexagon having side-length 3.5cm?
Solution:
Given that: s = 3.5cm.
A regular hexagon has 6 sides of the same length.

Hence, the perimeter of the regular hexagon is:
P = 6 * length
P = 6 * 3.5
P = 21cm

Online Perimeter Calculator
Web-Formulas.com © 2021 | Contact us | Terms of Use | Privacy Policy | Yellow Sparks Network
Web Formulas