Perimeter of a Parallelogram
Perimeter of a Parallelogram:

h: height
For any parallelogram the following statements are true:
ab = dc
ad = bc
The perimeter of a parallelogram is therefore given by:
P = 2 (ad + ab)
If the length of ad or bc is not given, it can be calculated by using the following formula:
ad = bc = h/cos(∠ecb)
where ∠ecb is the angle measured in degree or radian
∠ecb can be calculated if the length of eb is given:
∠ecb = tan-1(eb/h)
Example 1: Find the area and perimeter of the parallelogram, whose base is 18 cm and the height is 4 cm, also the angle between the base and the side is 130o and 50o.

Solution:
Given that:
base = dc = ab = 18 cm
h = 4 cm
Area of parallelogram:
A = b · h
A = 18 · 4
A = 72
Thus, area of parallelogram = 72 cm2
Perimeter of parallelogram:
P = 2(dc + ad)
Since the length of ad is not known, we need to determine it first using ad = bc = h/cos(∠ecb)
Inserting ∠ecb = 150 o – 90 o = 60o
ad = bc = 4/cos(∠60 o)
ad = bc = 8 cm
P = 2 · (18 + 8) = 2 ·26 = 52 cm
Example 2: The area of the parallelogram ABCD is 54 m2 and its perimeter is 34 m. What are the dimensions of the parallelogram?
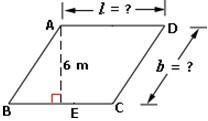
Solution:
Step 1: The area of the parallelogram ABCD = base × height = BC × AE = 54 m2 [Given, area of ABCD = 54 m2]
Step 2: From the figure above, we can see that the height of the parallelogram is AE = 6 m
Step 3: The base length of the parallelogram is BC = 54 · AE = 546 = 9 m[Substitute AE = 6.]
Step 4: The perimeter of the parallelogram = AB + BC + AB + BC [From the figure, since CD = AB and AD = BC.]
Step 5: [Substitute the value of the perimeter of the parallelogram.] (2 × AB) + (2 × BC) = 34
Step 6: [Distributive property.]2 × (AB + BC) = 34
Step 7: [Divide each side by 2.]AB + BC = 17
Step 8: [Substitute base length BC =9 m.]AB + 9 = 17
Step 9: [Subtract 9 from both the sides.]AB = 17 - 9 = 8 m
Step 10: The dimensions of the parallelogram are l = 9 m and b = 8 m.
Example 3: Find the perimeter of a parallelogram whose slant height is 24, height is 22 and breadth is 26, all units are in measured in mm.
Solution:
Given that:
a = slant height of the parallelogram
b= breadth of the parallelogram
Perimeter of a parallelogram = 2*(24+26) = 2*50 = 100 mm
Example 4: Find the perimeter of the parallelogram ABCD.
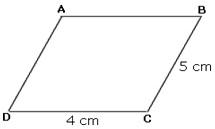
Solution:
Perimeter of the parallelogram ABCD = AB + BC + CD + AD
AB = DC = 4 cm and AD = BC = 5 cm
Perimeter = 4 + 5 + 4 + 5 = 18 cm
Online Perimeter Calculator