Example 1:
Find the area of a parallelogram with base 24 m and height 17 m.
Solution:
A = bh
A =24 * 17
A = 408 m2
Example 2: The base of a parallelogram is 15 cm and the height is 10cm. What are the area and perimeter of this parallelogram?
Solution: We know the area is
A = bh
A = 15 * 10
A = 150cm2
As show below we do not have any information about the left and right sides.
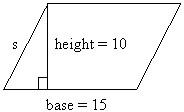
Thus, we cannot determine the perimeter.
Example 3: A parallelogram has a base of 3x, a height of x, and the other side of the parallelogram (not the base) is 2x. If the area of this parallelogram is 15, what is its perimeter?
Solution:
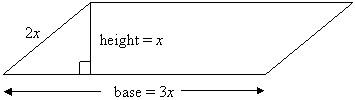
Notice in the diagram that we know enough information to formulate an equation for the area of the parallelogram.
A = bh = (3x)x = 3x2
A = 15
3x2 = 15
x2 = 5
x = √5
Since x = √5, we know the height h = √5, the base b = 3x = x√5 and the other side is 2x = 2√5.
The perimeter is the sum of the four sides, namely the two bases and two other sides.
Perimeter = 2 * (3 * √5) + 2 * (2 *√5 ) = 10√5
Example 4: A parallelogram is 3 yards long. The height, measured perpendicular to this side, is 1.5 yards. What is the area?
Solution: Since they are perpendicular, the side measurement and the height can be used in the formula.
A = 3 * 1.5
A = 4.5 square yards.
Example 5: Determine the area of a parallelogram that is 5 m high whereas the base is 9 m long.
A = b ∙ h = 9 ∙ 5 = 45 m2
Online Area Calculator