Example 1: Integrate: ∫sin1/3x cosx dx
Solution:
We could either choose u = sin x, u = sin1/3x or u = cos x. However, only the first one of these works in this problem.
So we let u = sin x.
Finding the differential:
du = cos x dx
Substituting these into the integral gives:
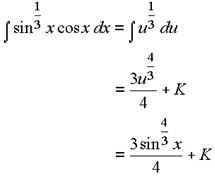
Example 2: Evaluate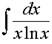
Solution:
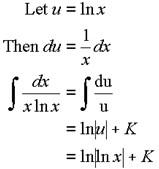
Example 3: Evaluate ∫15678dx
Solution:
∫15678dx = 15678x+C
Example 4: Evaluate ∫6x2 + 4dx
Solution:
∫6x2 + 4dx
= 6∫x2dx + 4∫dx
=6x3/3 + 4x + C
= 2x3 + 4x + C