Example 1: Evaluate 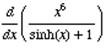
Solution: Use the quotient rule
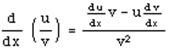
where u = x6 and v = sinh(x) +1
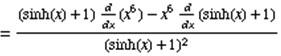
The derivative of a sum is the sum of the derivatives.
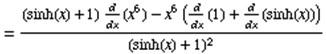
The derivative of the constant 1 is 0.
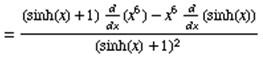
The derivative of sinh(x) is cosh(x)
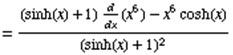
The derivative of x6 is 6x6-1
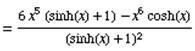
Simplify the equation we get:
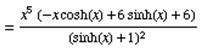
Example 2: Differentiate each of the following functions
a) f(x) = 2x5cosh(x)
b) h(t) = sinh(t)/(t+1)
Solution:
a) f´(x) = 10x4cosh(x) + 2x5sinh(x)
b) 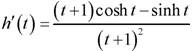
Example 3: Find the derivative of f(x) = sinh (x 2)
Solution :
Let u = x 2 and y = sinh u and use the chain rule to find the derivative of the given function f as follows.
f '(x) = (dy / du) (du / dx)
dy / du = cosh u, see formula above, and du / dx = 2 x
f '(x) = 2 x cosh u = 2 x cosh (x 2)
Substitute u = x 2 in f '(x) to obtain
f '(x) = 2 x cosh (x 2)