Algebraic Operations on Complex Numbers

In performing operations with complex numbers we can proceed as in the algebra of real numbers replacing i² by -1 when it occurs.

1.   Addition of Complex Numbers

(a+bi) + (c+di) = (a+c) + (b+d)i 

Example:
z1 = 3 - 4i and z2 = -2 + 2i
z1 + z2 = (3 + (-2)) + (-4 + 2)i = 1 -2i

2.   Subtraction of Complex Numbers

(a+bi) - (c+di) = (a-c)+ (b-d)i

Example:
z1 = 3 - 4i and z2 = -2 + 2i
z1 - z2 = (3 - (-2)) - (-4 - 2)i = 5 +6i

3.   Multiplication of Complex Numbers

(a+bi)(c+di) = ac+bci+adi+bdi²

        = (ac-bd)+(ad+bc)i

Example:
z1 = 3 - 4i and z2 = -2 + 2i
z1 ∙ z2 = (3 ∙ (-2)) + (-4 ∙ (-2))i + (3 ∙ 2)i + (-4 ∙ 2)i² = -6 + 14i -8i²

4.   Division of Complex Numbers

(a+bi)/(c+di)=(a+bi)/(c+di)×(c-di)/(c-di)
                    =(ac-adi+bci-bdi²)/(c²-d²i²)
                    =(ac+bd+(bc-ad)i)/(c²-d²i²)
                    =(ac+bd)/(c²+d² )+(bc-ad)/(c²+d²) i

Example:
z1 = 3 - 4i and z2 = -2 + 2i
z1 / z2 = (3 ∙ (-2) + (-4 ∙ 2))/((-2)² + 2²) + (-4 ∙ (-2) - 3 ∙ 2)/((-2)² + 2²)i = -14/8 + (2/8)i = -7/4 + i/4

Inequalities in imaginary numbers are not defined. As for example z >0, 4 + zi < 2+4i are meaningless in complex numbers.

In real numbers, if a² + b²=0 then a=b=0; however in complex numbers,

z₁² + z₂² does not imply z₁ = z₂ = 0

Complex conjugation: The complex conjugate of a + bi is a − bi. The importance of the complex conjugate lies in the fact that the product of a complex number and its conjugate is a real number.

(a + bi)(a − bi) = (a  + b)

Additive identity: Additive identity is the complex number that represents the notion of zero for addition of complex numbers is 0 + 0i.

(a + bi) + (0 + 0i) = a + bi

Multiplicative identity: Multiplicative identity is the complex number that represents the notion of one for multiplication of complex numbers is 1+ 0i.

 (a + bi)(1+ 0i) = a + bi

Example 1: Simplify (2√(-9) -3 )(3√(-16) - 1)

(2√(-9) -3 )(3√(-16) - 1)

=(2 · 3i - 3)(3 ·4i - 1)

=(6i - 3)(12i - 1)

= 72i² – 36i – 6i + 3

= -69 – 42i

Example 2: Express in the form a + bj given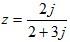

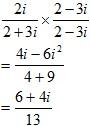
Example 3: Perform the division for the complex numbers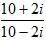
Solution: The given complex numbers are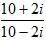

We have to reduce the denominator as well as the numerator by multiplying the numerator and denominator both by the complex number 10+2i.

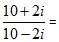
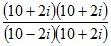
Use the formula (a+ b) (a-b) = a²- b² to reduce the denominators. Use the formula (a+ b) ²= a²+2ab+ b² to reduce the numerators.

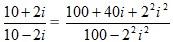
Add and also square the terms to get the values.

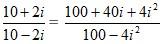
In the complex numbers the value for i² is -1.

Substitute the value of i² in the above equation to reduce the denominators.

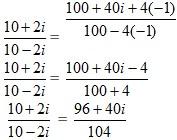
Example 4: Find the product of the complex numbers 1+ i and √ 3- i in polar form.

Solution: We can easily find that the polar form of 1+ i and √ 3- i are respectively,

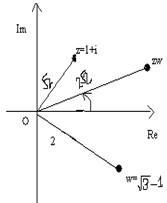
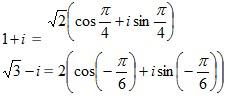
We know that z₁z₂ = r₁r₂(cos(θ₁+θ₂) + isin(θ₁ + θ₂)). This formula says that to multiply two complex numbers we need to multiply the moduli and add the arguments. Therefore multiplying 1+ i and √ 3- i using the above rule, we will get:

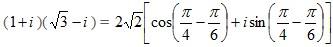
Example 5: Simplify i^64,002.