Equality: Two complex numbers are equal if and only if their real parts and their imaginary parts are respectively equal.

a+ib =c+id  if and only if a=c and b=d

Example 1: If x+4yi+40 = 5x+8i, Find the values x and y.

Solution: Equating the left hand side of the real part = Right hand side of the real part

x +40 = 5x

5x-x = 40

4x=40

x=10

Left hand side of the imaginary part = Right hand side of the imaginary part

4y = 8

y = 2

Therefore the value x is 10 and the value y is 2.

Example 2: Find the values of a and b for the following equations:

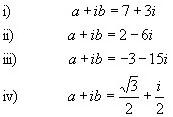
Solution:

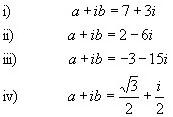
Example 3: If z = x + iy and |2z- 1| = |z- 2| then prove that x² + y² = 1.
Solution :

|2z- 1| = |z- 2|

→|2(x+iy)- 1| = |x+iy- 2| 
→|(2x-1)+2iy| = |(x-2)+iy| 
→√(2x − 1) 2 + 4y2 = √(x − 2)2+ y2 
→4x2 - 4x + 1 + 4y2 = x2 − 4x + 4 + y2

(squaring on both sides) 
→3x2 + 3y2 - 3 = 0 
→3x2 + 3y2 = 3 
→x2 + y2 = 1. (Proved).

Example 4: Find the real numbers a and b such that the equation below becomes true.

(a + 6) + 2bi = 4 - 5i

Solution: (a + 6) + 2bi = 4 - 5i

Equating the real and imaginary parts, we get,

            a + 6 = 4  and  2b = -5

            a = -2       and    b = -5/2