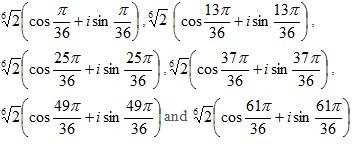A complex number is made up of both real and imaginary components. It can be represented by an expression of the form (a+bi), where a and b are real numbers and i is imaginary. When defining i we say that i = √(-1). Along with being able to be represented as a point (a,b) on a graph, a complex number z = a+bi can also be represented in polar form as written below:
z = r (cos θ + i sinθ)
where r = [z] = √(a2 + b2)
and
θ = tan-1(b/a) or θ = arctan(b/a)
and we also have: a = r cosθ and b = r sinθ
Statement of DeMoivre's Theorem
Let 'n' be any rational number, positive or negative, then
[cos θ + i sin θ ]n = cos nθ + i sin nθ
Basically, in order to find the nth power of a complex number we need to take the nth power of the absolute value or length and multiply the argument by n.
Let z = r (cos θ + i sinθ) and n be a positive integer. Then z has n distinct nth roots given by: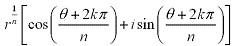
, where k = 0, 1, 2, ... , n-1
De Moivre's Theorem states that for any complex number as given below:
z = r ∙ cosθ + i ∙ r ∙ sinθ
the following statement is true:
zn = rn (cosθ + i ∙ sin(nθ)), where n is an integer.
If the imaginary part of the complex number is equal to zero or i = 0, we have:
z = r ∙ cosθ and zn = rn (cosθ)
Exponential form of complex number:
z = reiθ where r is the modulus of z and θ is its argument.
Example 1: Compute the three cube roots of -8.
Solution: Since -8 has the polar form 8 (cos π + i sin π), its three cube roots have the form
3√8 {cos[(π + 2πm)/3] + i sin[(π + 2πm)/3]} for m=0, 1, and 2.
Thus the roots are
2 (cos π/3 + i sin π/3) = 1 + √3 i,
2 (cos π + i sin π) = -2, and
2 (cos 5π/3 + i sin 5π/3) = 1 - √3 i.
Example 2: Use De Moivre's Theorem to compute (1 + i)12.
Solution: The polar form of 1 + i is √2 (cos π/4 + isin π/4). Thus, by De Moivre's Theorem, we have:
(1 + i)12 = [√2 (cos π/4 + i sin π/4)]12
= (√2)12(cos π/4 + i sin π/4)12
= 26 (cos 3π + i sin 3π)
= 64(cos π + i sin π)
= 64(-1) = -64.
Example 3: Use De Moivre's Theorem to compute (√3 + i)5.
Solution: It is straightforward to show that the polar form of √3 + i is 2(cos π/6 + i sin π/6). Thus we have:
(√3 + i)5 = [2(cos π/6 + i sin π/6)]5
= 25(cos π/6 + i sin π/6)5
= 32(cos 5π/6 + i sin 5π/6)
= 32(-√3/2 + 1/2 i)
= -16√3 + 16 i.
Example 4: Find the sixth roots of √3+i
Solution: The modulus of √3+i is 2 and the argument is π/6.
The sixth roots are therefore