Properties of Inverse Matrices
Properties of Inverse Matrices:
If A is nonsingular, then so is A -1 and (A -1) -1 = A
If A and B are nonsingular matrices, then AB is nonsingular and (AB) -1 = B-1 A -1
If A is nonsingular then (AT)-1 = (A-1)T
If A and B are matrices with AB=In then A and B are inverses of each other.
Notice that the fourth property implies that if AB = I then BA = I
Let A, A1 and A2 be n×n matrices, the following statements are true:
1. If A-1 = B, then A (col k of B) = ek
2. If A has an inverse matrix, then there is only one inverse matrix.
3. If A1 and A2 have inverses, then A1 A2 has an inverse and (A1 A2)-1 = A1-1 A2-1
4. If A has an inverse, then x = A-1d is the solution of Ax = d and this is the only solution.
5. The following are equivalent:
(i) A has an inverse.
(ii) det (A) is not zero.
(iii) Ax = 0 implies x = 0.
If c is any non-zero scalar then cA is invertible and (cA)-1 = A-1/c.
For n = 0, 1, 2…, An is invertible and (An)-1 = A-n = (A-1)n.
If A is a square matrix and n > 0 then:
A-n = (A-1)n
Example 1: Compute A-3 for the matrix:
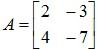
Solution: First of all, we need to find the inverse of the given matrix. The method to find the inverse is only applicable for 2 × 2 matrices.
Steps are as follows:
[1] Interchange leading diagonal elements:
-7 → 2
2 → -7
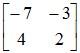
[2] Change signs of the other 2 elements:
-3 → 3
4 → -4
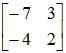
[3] Find the determinant |A|
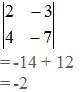
[4] Multiply result of [2] by 1/|A|
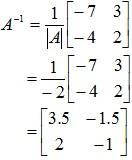
Now: 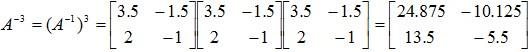
Example 2: Given the matrix A verify that the indicated matrix is in fact the inverse.
Solution:

To verify that we do in fact have the inverse we’ll need to check the condition
AA-1 = A-1A = I
Now we check whether AA-1 = A-1A = I:
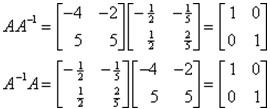
Hence the required is verified.
Example 3: Let A be the 2 × 2 matrix,
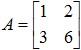
Show that A has no inverse.
Solution: An inverse for A must be a 2 × 2 matrix.
Let 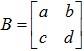 such that AB = BA = I. If such a matrix B exists, it must satisfy the following equation:
such that AB = BA = I. If such a matrix B exists, it must satisfy the following equation:
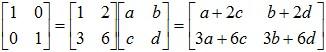
The preceding equation requires that:
a + 2c = 1 and 3a + 6c = 0
which is clearly impossible, so we can conclude that A has no inverse.