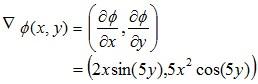Gradient of a Scalar Field
The gradient of a scalar field is a vector field and whose magnitude is the rate of change and which points in the direction of the greatest rate of increase of the scalar field. If the vector is resolved, its components represent the rate of change of the scalar field with respect to each directional component. Hence for a two-dimensional scalar field ∅ (x,y).
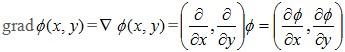
And for a three-dimensional scalar field ∅ (x, y, z)
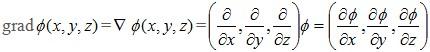
The gradient of a scalar field is the derivative of f in each direction. Note that the gradient of a scalar field is a vector field. An alternative notation is to use the del or nabla operator, ∇f = grad f.
For a three dimensional scalar, its gradient is given by:
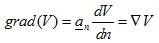
Gradient is a vector that represents both the magnitude and the direction of the maximum space rate of increase of a scalar.
dV = (∇V) ∙ dl, where dl = ai ∙ dl
In Cartesian
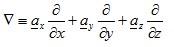
In Cylindrical
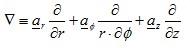
In Spherical
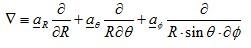
Properties of gradient
· We can change the vector field into a scalar field only if the given vector is differential. The given vector must be differential to apply the gradient phenomenon.
· The gradient of any scalar field shows its rate and direction of change in space.
Example 1: For the scalar field ∅ (x,y) = 3x + 5y,calculate gradient of ∅.
Solution 1: Given scalar field ∅ (x,y) = 3x + 5y
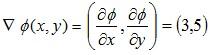
Example 2: For the scalar field ∅ (x,y) = x4yz,calculate gradient of ∅.
Solution: Given scalar field ∅ (x,y) = x4yz
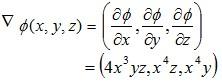
Example 3: For the scalar field ∅ (x,y) = x2sin5y,calculate gradient of∅.
Solution: Given scalar field ∅ (x,y) = x2sin5y