Introduction:
Conductor is a substance or object that allows electricity to flow through it with low resistance. “Conductor” implies that the outer electrons of the atoms are loosely bound and free to move through the material. Conductivity of conductors is between semiconductors and superconductors. Under static conditions the E field on the conductor surface is always perpendicular to the surface.
Under Static Electric Field:
Assume that some positive (or negative) charges are introduced in the interior of a conductor. An electric field will be set up in the conductor; the field exerts a force on the charges and makes them move away from one another. This movement will continue until all the charges reach the conductor surface and redistribute themselves in such a way that both the charge and the field inside vanish.

Since E field can be expressed as:
E = -ΔV, if E= 0, the integral of V must be a constant, thus for E = 0, the voltage must be the same everywhere in the conductor.
If we put a conductor in a static electric field in the beginning the electric field will penetrate inside the material. As time passes the free electrons in the conductor will move in the opposite direction of the electric field and the holes will move in the same direction with the electric field which causes the positive charges and negative charges being collected on opposite sides of the material creating a field opposing the static electric field and a current density in the same direction with the electrostatic field. We can investigate the current density formula and the below graph for a better understanding of these situations.
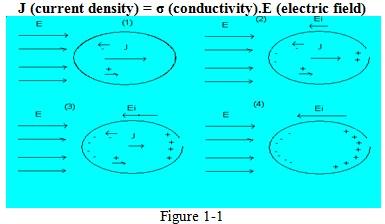
In part (1) the electric field is penetrating through the material causing a current density in the same direction.
In part (2) as a result of the current in the material there happens to be an electric field opposing the external electric field so now only part of the external electric field is penetrating and the magnitude of the current density got smaller (can be seen by looking at the formula). The electric field inside the material is still in the + x direction with a magnitude equal to E - Ei.
In part (3) the same action continues as in part (2) and J gets smaller and Ei gets bigger. As a result the electric field penetrating through the material got even smaller than part (2).
In part (4) E = Ei which means there is no more electric field in the material and the current density is zero. We can see that the negative charges are collected on the left side and positive charges on the right that creates a potential difference and the electric field Ei. We have to remember that and electric field is from positive to negative, the external electric field attracted the electrons to its source and repelled the protons away from its source.
The charge distribution on the material depends on the shape of the material and there will never be tangential component of electric field on the surface because it would cause the charges on the surface to move. That means under static conditions the E field on a conductor surface is everywhere normal to the surface which makes its surface an equipotential surface.
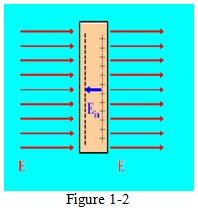
In the above picture there is another conductor and in static condition E equals Ein so that the net electric field inside the material is zero.
Ein is the electric field created by the charges inside the material and if we take the external electric field (E) away the charges will redistribute inside the material making the internal electric field zero again. The redistribution process takes a certain amount of finite time depending on the conductivity of the material.
Example (1): Under static conditions, what will be the electric field and charge in a conductor?
Solution: Under static conditions, both the electric current and the charge in a conductor will be zero.
Example (2): Under static conditions, what will be the normal and the tangential component of the electric field is equal to on the surface of a conductor?
Solution: Under static conditions, the tangential component of the electric field is always zero on the surface and the normal component is equal to surface charge density on the conductor divided by the permittivity of space.
Example (3): Where do most static electric charges collect?
(a)In a copper wire
(b)On the surface of a non-conductor
(c)In a spark
Answer :(b)
Example (4): Which of the following will usually create static electricity?
(a)Rub a wet rag on a plastic comb
(b)Rub a coin with a plastic comb
(c)Rub a plastic comb with some rabbit fur
Answer :( c)
Example (5): What can cause electrons to jump across a gap and cause a spark?
(a)The force from a large positive charge on the other side of the gap
(b)Lightning causes many things to happen
(c)Heating up the gap
Answer :( a)