Application of Gauss’s Theorem
Application of Gauss’s Theorem
Electric field due to an infinite long straight charged line:
Consider one example of an infinite long straight charged line having uniform linear charge density (λ) and a point P located at a perpendicular distance r from the linear charge distribution. The electric field intensity at any point P and all the other points like P situated perpendicular distance from the line will be equal as the line is of infinite length (L).
As per Gauss’ law, the electric field intensity at point P on an infinitely long straight charged line is:
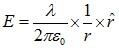
Here we have
λ = linear charge density
ε0 = electrical permittivity of free space
r = radius
ȓ = unit vector in the direction of radius.
Electric field due to a uniformly charged infinite plane sheet:
Consider one example of a uniform charged infinite plane sheet having uniform surface charge density σ, point P situated at a perpendicular distance r from the given plane, then the electric filed intensity as per the Gauss’ law is:
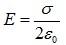
Here we have
σ = Surface charge density
ε0 = electrical permittivity of free space
It shows that the electric field intensity at any point on the plane sheet is not depend on the distance of the point from the plane.
Electric field due to a uniformly charged thin spherical shell:
Consider a spherical shell having surface charge density σ and radius R. The electric field resulting from such a spherical shell is radial and hence electric field intensity is calculated for a point lying inside and outside the spherical shell.
Point lying inside the shell:
Here point is lying inside the shell and having radius r smaller then the spherical shell radius R. So, as per the Gauss’ law, the electric field intensity is zero due to charge enclosed by such a surface is zero as the radius is concentric with the shell.
Point lying outside the shell:
Here point is lying outside the shell and having radius r greater then the spherical shell radius R. So, as per the Gauss’ law, the electric field intensity is,
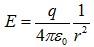
It shows that for a point outside the sphere, the entire charge of the sphere can be treated as concentrated at its centre.
Electric field due to a uniformly charged sphere:
Consider a uniformly charged sphere having volume charge density ρ and radius of sphere R. The electric field resulting from such a sphere is radial and hence electric field intensity is calculated for a point lying inside and outside the spherical shell.
Point lying inside the shell:
Here point is lying inside the sphere and the spherical Gaussian surface of radius r < R, concentric with the sphere. Using Gauss’ law, the electric field intensity is
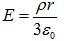
Point lying outside the shell:
Here point is lying outside the sphere and the spherical Gaussian surface of radius r > R, coincide with the each other. Using Gauss’ law, the electric field intensity is
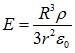
Calculation:
Example-1: A particle having surface charge density 4 x 10-6 c/m2, is held at some distance from a very large uniformly charged plane. Calculate the electric field intensity at any point lying on uniformly charged plane. Here ε0 = 8.85 x 10-12 C2N-1m-2.
Reason:
ε0 = 8.85 x 10-12 C2N-1m-2
σ = 4 x 10-6 c/m2
E = σ / (2 ε0)
E = 4 × 10-6 / (2 × 8.85 × 10-12)
E = 2.26 × 105 NC-1
Example-2: Electric field intensity due to a uniformly charged infinite plane sheet is depends on....................
a) Surface charge density
b) Electrical permittivity
c) Radius
d) Surface charge density and electrical permittivity.
Answer: Electric field intensity due to a uniformly charged infinite plane sheet is depends on surface charge density and electrical permittivity.
Example-3: Gauss’ theorem depends on...............................
a) total electrical flux linked with any closed surface
b) integration of electric field over a closed surface
c) total electric charge associated with closed surface
d) none of above
Answer: Gauss’ theorem depends on integration of electric field over a closed surface