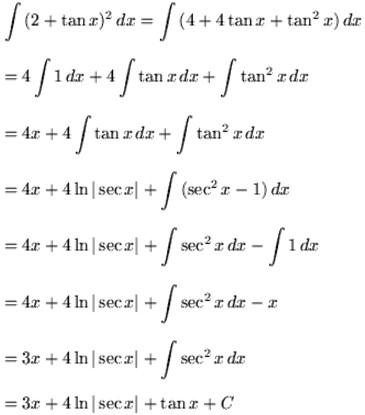Current Location  >  Math Formulas > Calculus > Integrals of Trigonometric Functions

Integrals of Trigonometric Functions
Function Integral
sinx -cosx + c
cosx sinx + c
sin2x x/2 - sin(2x)/4 + c = (x - sinx ∙ cosx)/2 + c
cos2x x/2 + sin(2x)/4 + c = (x + sinx ∙ cosx)/2 + c
tanx = sec2x -ln|cosx| + c
cotx = -csc2x ln|sinx| + c
secx ln|secx + tanx| + c
cscx -ln|cscx + cotx| + c
sec2x tanx + c
csc2x -cotx + c

Example 1: Calculate the following integral ∫x2 sinx3dx.
Solution:
∫x2 sinx3dx = ∫ sinx3 x2 dx
Set u = x3 and du = 3x2dx or du/3 = x2dx, then we have:
∫x2 sinx3 dx
= ∫sinu du/3
= 1/3 * ∫sinu du
= 1/3 *(-cosu) + C
= 1/3 *(-cosx3) + C

Example 2: Calculate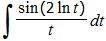
Solution:
Let u = ln t. So du = (1/t) dt.
We then have:



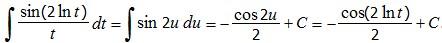
Example 3: Evaluate ∫(3sin x 4sec2x) dx
Solution:
∫(3sinx 4sec2x) dx
= 3∫sinxdx - 4∫sec2x dx
= -3cosx – 4tanx + C

Example 4: Integrate ∫(2+ tanx)2 dx
Solution:




Web-Formulas.com © 2012 | Contact us | Terms of Use | Privacy Policy | Yellow Sparks Network
Web Formulas