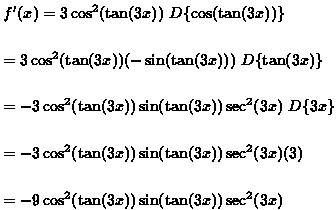General Differentiation
|
Function
|
Derivative
|
|
sinx
|
cosx
|
|
cosx
|
-sinx
|
|
sin2x
|
2∙sinx∙cosx = sin2x
|
|
cos2x
|
-2∙sinx∙cosx = - sin2x
|
|
tanx = sec2x
|
1/(cos2x) = 1+tan2x
|
|
cotx = -csc2x
|
-1/(sin2x) = -1-cot2x
|
|
secx
|
secx∙tanx
|
|
cscx
|
-cscx∙cotx
|
|
arcsinx = sin-1x
|
1/√(1-x2)
|
|
arccosx = cos-1x
|
-1/√(1-x2)
|
|
arctanx = tan-1x
|
1/(1+x2)
|
|
arccotx = cot-1x
|
-1/(1+x2)
|
|
arcsecx = sec-1x
|
1/(|x|∙√(x2-1))
|
|
arccscx = csc-1x
|
-1/(|x|∙√(x2-1))
|
The following table summarizes the derivatives of the six trigonometric functions, as well as their chain rule counterparts (that is, the sine, cosine, etc. of a function).
Example 1:
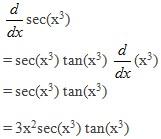
Example 2: Find the derivative of y = 3 sin3 (2x4 + 1).
Put u = 2x4 + 1 and v = sin u
So y = 3v3
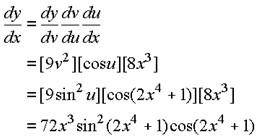
Example 3: Differentiate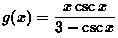
Apply the quotient rule first, then we have
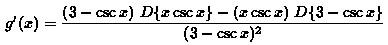
Now apply the product rule in the first part of the numerator, the result of g'(x) will be:
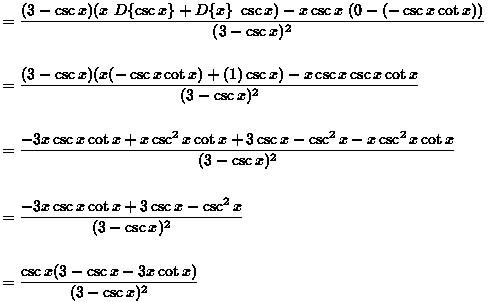
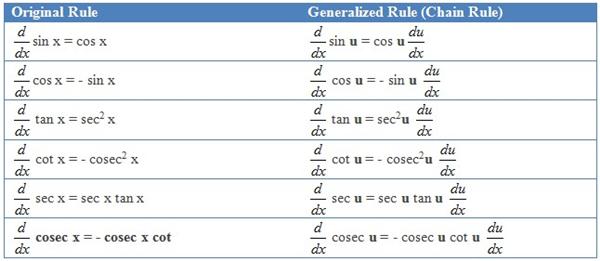
Example 4: Differentiate y = cos3(tan(3x)).
Apply the chain rule four times: