An exponential function f is defined by

f(x) = c^x,

where c > 0 and c ≠1. The exponent x is any real number and f is called an exponential function.

Again, note that the variable x is in the exponent as opposed to the base when we are dealing with an exponential function.  Also note that in this definition, the base c is restricted to being a positive number other than 1.

The exponential function with base e is called the natural exponential function and e has a value attached it (similar to pi), which in this case is approximately 2.718281828...  This base is used in economic analysis and problems involving natural growth and decay. 

For natural exponential functions the following rules apply:

Note e^x can be denoted as e^x as well

exp(x) = ex = e^{ln(e^x)}

exp_a(x) = e^{x ∙ ln a} = 10^{x ∙ log a} = a^x

exp_a(x) = a^x

Graphing Exponential Functions:

Step 1: Find ordered pairs:

I have found that the best way to do this is to do the same each time.  In other words, put in the same values for x each time and then find its corresponding y value for the given function.
 

Step 2: Plot points:

This is done exactly the same way we plotted points when we graphed lines and parabolas.

Step 3: Draw curve: 

The basic curve of an exponential function looks like the following:

Introduction to asymptotes of exponential functions

In certain functions, either the value of the function tends to infinity (or –infinity) for an input variable or the function tends to a constant value at an infinitely small (or large) value of the input variable. There are also cases when both happen.

Graphically, the curve of the function in these cases is contained within a (or a set of) line. Such a line (or set of lines) is called the asymptote of the function.

Let us take a look at the asymptotes of exponential functions.

Asymptotes of Exponential Functions - Concept

An exponential function is that function which varies with the independent variable appearing as an exponent. That is, f(x) = a^x, where a is a positive constant and is not equal to 0 or 1.

In a more generalized way, an exponential function is given as, f(x) = a^x+ b, where a and b are constants where a is positive and not equal to 0 or 1. ( If a is negative, the function can not be exponential as the function will be negative for odd values of x and positive for even values of x. Similarly if x is 0 or 1, the function becomes constant as f(x) = b and f(x) = 1 + b, respectively.)

Rewriting the function, a^x = f(x) - b

The value of the power expression a^x can only be positive.

Therefore we have:

a^x > 0

 f(x) – b > 0

f(x) > b

This means that the value of the function tends to a constant value, which in this case is b.

Also f(x) tends to b, when a^x tends to 0 which happens when x become infinitely smaller. In other words, the function tends to the constant value when x tends to minus infinity. This concept helps to find the asymptotes of exponential functions, which is shown as below:

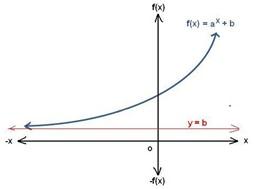
The curve represents the general form of an exponential function.

As x becomes smaller and smaller, the curve tends to become a straight line. In other words, the curve will always be above the horizontal line f(x) = b, shown in red. This line is called the asymptote of the exponential function.

Asymptotes of exponential functions are always horizontal lines and hence it can be concluded that an exponential function has only one horizontal asymptote.

If the value of b is 0, then x-axis is the asymptote of the exponential function. If it is negative, then the asymptote will be below and parallel to the x-axis.

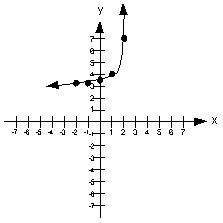
Example 1:  Graph the function f(x) = 4 ^x-1 + 3.

Note that in this case the base is 4 and the exponent is x - 1.

Step 1: Find ordered pairs.
 

I have found that the best way to do this is to do it the same each time.  In other words, put in the same values for x each time and then find its corresponding y value for the given function.
 

Step 2: Plot the points and draw the curve. 

Example 2: The population of bacteria in a culture is growing exponentially. At 12:00 there were 80 bacteria present and by 4:00 PM there were 500 bacteria. Find an exponential function f(t) = ke^at that models this growth, and use it to predict the size of the population at 8:00 PM.

Solution

Let t = 0 at 12:00 noon, then at 4:00 PM, t = 4 and at 8:00 PM t = 8. You need to find the values of the parameters k and a. k is easy in this case (and many others) because you are given the population value f(0). Notice that at t = 0 we have f(0) = ke^0*a = k*1 = k. Thus k = 80.
To find a, substitute t = 4, f(4) = 500 since k = 80 we have 500 = 80e^4a. Dividing both sides by 80 and taking logarithms you will get a = ln (6.25) / 4 = .4581

This gives the function f(t) = 80 e^{.0.4581 t},  and for t = 8 we have f(8) = 80 e^.4581*8 = 3,125

Thus, the exponential function is f(t) = 80 e^{.4581 t} and there will be 3,125 bacteria at 8:00 PM.   

Example 3:

Solution