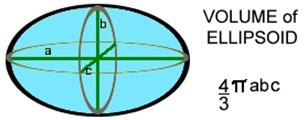
In the same way that a circle turns into a solid sphere, an ellipse can become a solid "ellipsoid".
There are two special types of ellipsoid.

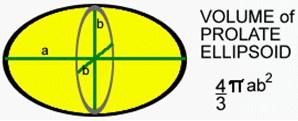
Suppose if we have a sphere and stretch it to make a longer and thinner shape (a bit like a rugby ball or a melon). In such case it is called a prolate ellipsoid. If we chop it in half to get a circle, then the volume is the area of the circle times 2/3rd of the major axis. (The major axis is the maximum length from the one end to the other.)

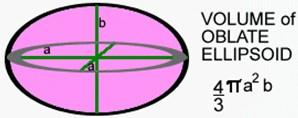
However if we have a sphere and squash it to make a shorter fatter shape (a bit like a burger). In such case it is called an oblate ellipsoid. If we chop it through the middle to get a circle, then the volume is the area of the circle times 2/3rd of the minor axis.

Example 1: An ellipsoid whose radius and its axes are a= 21 cm, b= 15 cm and c = 2 cm respectively. Determine the volume for the given ellipsoid.
Solution:
Volume of ellipsoid:
V = 4/3 × π × a × b × c
V = 4/3 × π × 21 × 15 × 2
V = 2640 cm³

Example 2: The ellipsoid whose radii are given as r₁ = 9 cm, r₂ = 6 cm and r₃ = 3 cm. Find the volume of ellipsoid.
Solution:
Radius (r₁) = 9 cm
Radius (r₂) = 6 cm
Radius (r₃) = 3 cm
The volume of the ellipsoid:
V = 4/3 × π × r₁ × r₂ × r₃
V = 4/3 × π × 9 × 6 ×3
V = 678.24 cm³
Volume of ellipsoid (V) = 678.24 cubic units

Example 3: An ellipsoid whose radii are given as r₁ = 12 cm, r₂ = 10 cm and r₃ = 9 cm. Find the volume of the ellipsoid.
Solution:
Radius (r₁) = 12 cm
Radius (r₂) = 10 cm
Radius (r₃) = 9 cm
The volume of the ellipsoid:
V = 4/3 × π × r₁ × r₂ × r₃
V = 4/3 × π × 12 × 10 ×9
V = 4521.6 cm³