The electric field or electric field strength is the electrostatic force acting on a small positive test charge placed at that point. If 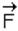is the electrostatic force experienced by a test charge q at a point, then the electric field intensity at that point is given by

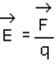
S.I unit of electric field intensity is Newton/coulomb (NC^-1).

If the test charge is not small, then the electric field may be affected by the test charge and hence we modify the above equation as follows:

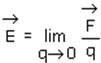
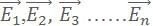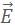Consider a system of charges q₁, q₂, ………..q_n placed at distances r₁, r₂….r_n with respect to some origin. Then the electric field intensity due to all these charges at a point is found out using the Principle of superposition. Let  intensity due to the number of charges q₁, q₂, ………..q_n. Then the resultant electric intensity  at that point due to these charges is given by the superposition theorem.

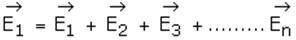
Electric field intensity due to the n^th charge is

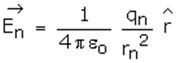
Magnitude of the electric field intensity is given by the equation:

Example1: Two point charges of 1μC and -1 μC are separated by a distance of 100 Å. A point P is at a distance of 10 cm from the midpoint and on the perpendicular bisector of the line joining the two charges. The electric field at P will be

(a)    9 N/C

(b)   0.9 V/m

(c)    90 V/m

(d)   0.09 N/C

Solution: The point lies on equatorial line of a short dipole. So, 

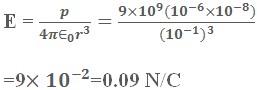
Example2: Three charges 2q,-q and –q are located at the vertices of an equilateral triangle .At the center of the triangle

(a)    the field is zero but potential is non-zero.

(b)   the field is non-zero ,but potential is zero.

(c)    both field and potential are zero.

(d)   both field and potential are non zero.

Solution: (b)

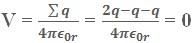
Obviously, E ≠ 0.Hence the field is non-zero but potential is zero.

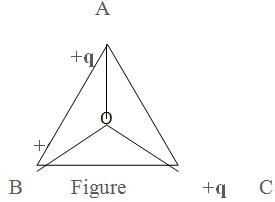
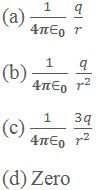
Solution: Unit Positive charge at O will be repelled equally by three charges at the three corners of triangle

By symmetry, resultant 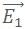at O would be zero.