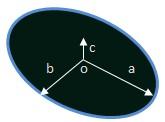
Surface Area of an Ellipsoid
The ellipsoid got its name because its cross sections parallel to the xy, xz and yz planes are all ellipses. It has the interesting property that it is regular everywhere except at the north and the south poles. Note also that its parameterization looks much like that of a sphere, but stretched by the constants a, b and c in the x, y and z directions.
If a, b, and c are the principal semiaxes, the general equation of such an ellipsoid is
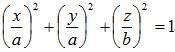
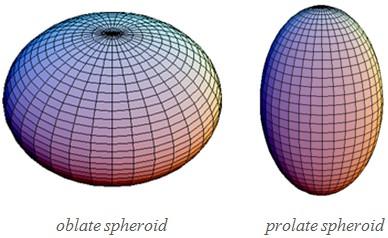
where a is the horizontal and transverse radius at the equator, and b is the vertical and conjugate radius. A special case arises when a = b = c: then the surface is a sphere and the intersection with any plane passing through it is a circle. If two axes are equal, say a = b and are different from the third axis c, then the ellipsoid is an ellipsoid of revolution, or spheroid, the figure is formed by revolving an ellipse about one of its axes. If a and b are greater than c, the spheroid is oblate; if less, the surface is a prolate spheroid.
An oblate spheroid is formed by revolving an ellipse about its minor axis, whereas a prolate spheroid is formed by revolving an ellipse about its major axis. In either case, intersections of the surface by planes parallel to the axis of revolution are ellipses, while intersections by planes perpendicular to that axis are circles.
A prolate spheroid has surface area defined as:
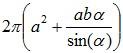
where,
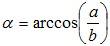is the angular eccentricity of the prolate spheroid and e = sin(α) is its (ordinary) eccentricity.
An oblate spheroid has surface area defined as:
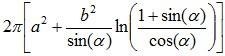where,
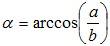is the angular eccentricity of the oblate spheroid.
A learning ellipsoid where its axis is not aligned is given by the equation
X T AX = 1
Here, A is the matrix where it is symmetric and positive definite and X is a vector.
In the ellipsoid formula 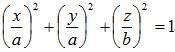, if all the three radii are equal then it is represented as a sphere. i.e. a = b = c.
a = b = c: sphere
a = b > c: oblate spheroid.
a = b < c: prolate spheroid
a > b > c: scalene spheroid.
The scalene ellipsoids are also called as “a triaxial ellipsoids” because all the three axes are required to be specified to define a shape.
Knud Thomsen’s Formula
According to wikipedia.org the surface area of a general ellipsoid cannot be expressed exactly by an elementary function. However an approximate formula can be used and is shown below:
a, b and c defines the vertical distances from the origin of the ellipsoid to its surface.
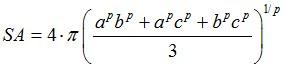
Where p ≈ 1.6075 yields a relative error of at most 1.061% (Knud Thomsen's formula)
π defines the ratio of any circle's circumference to its diameter and is approximately equal to 3.141593, however the value 3.14 is often used.
Example: determine the surface area of a ellipsoid that has following properties:
a = 2 m
b = 3 m
c = 4 m
SA = 4 ∙ π ∙ ((a1.6075b1.6075 + a1.6075c1.6075 + b1.6075c1.6075)/3)1/1.6075 = 111.604 m2
Online Surface Area Calculator, click on the link will open a new window.